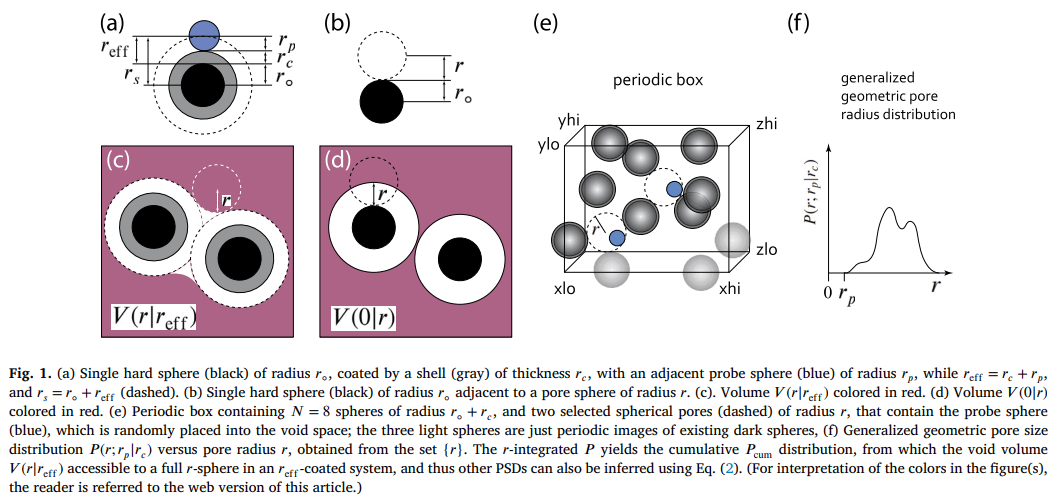
 The generalized geometric pore size distribution P(r;rp|rc) as function of pore radius r, probe sphere radius r, and coating thickness rc for a periodic two-dimensional system composed of circles (GPSD-2D) had been defined recently. For rp=rc it reduces to the widely accepted pore radius distribution P(r) introduced by Gelb and Gubbins. The three-dimensional counterpart GPSD-3D for periodic systems composed of spheres is implemented here using an efficient Voronoi-based semi-analytic strategy that offers significant advantages compared with both a grid-based implementation and constrained nonlinear optimization with respect to speed, precision and memory requirements. Moreover, GPSD-3D is fully parallelized using OpenMP.
for LaTeX users @article{MKroger2024-301,
author = {M. Kr\"oger and S. Agrawal and S. Galmarini},
title = {Generalized geometric pore size distribution code GPSD-3D for periodic systems composed of monodisperse spheres},
journal = {Comput. Phys. Commun.},
volume = {301},
pages = {109212},
year = {2024},
doi = {10.1016/j.cpc.2024.109212}
}
\bibitem{MKroger2024-301} M. Kr\"oger, S. Agrawal, S. Galmarini,
Generalized geometric pore size distribution code GPSD-3D for periodic systems composed of monodisperse spheres,
Comput. Phys. Commun. {\bf 301} (2024) 109212.MKroger2024-301
M. Kr\"oger, S. Agrawal, S. Galmarini
Generalized geometric pore size distribution code GPSD-3D for periodic systems composed of monodisperse spheres
Comput. Phys. Commun.,301,2024,109212 |
mk@mat.ethz.ch
1 out of 832 entries requested
[H-factor to-date: > 0]
